SCEST21: Schrodinger's Cat, and Einstein's Space-time, in the 21st Century
A blogspot for discussing the connection between quantum foundations and quantum gravity
Managed by: Tejinder Pal Singh, Physicist, Tata Institute of Fundamental Research, Mumbai
If you are a professional researcher / student researching on these topics, and would like to post an article here with you as author, you are welcome to do so. Please e-mail your write-up to tpsingh@tifr.res.in and it will be uploaded here.
Keywords: Quantum foundations; Quantum gravity; Schrodinger's cat; Spontaneous collapse theory;
Trace dynamics; Non-commutative geometry; Spontaneous quantum gravity; Classical general relativity
***************************
December 5, 2019
The theory of Spontaneous Quantum Gravity: an overview
YouTube Video https://youtu.be/lJk_mE8K8uw
Tejinder Singh
As we have seen in the previous posts, we would like an underlying theory for spontaneous collapse, which also provides a relativistic description of collapse. Trace dynamics goes a good part of the way, by deriving quantum field theory as the equilibrium statistical mechanics of an underlying matrix dynamics with global unitary invariance. Brownian motion fluctuations about equilibrium can provide the origin of spontaneous localisation, subject to a few assumptions. Trace dynamics operates at the Planck scale, but assumes space-time to be flat Minkowski space-time. Quantum theory is then derived by coarse graining trace dynamics over time scales much larger than Planck time. Quantum dynamics is thus a low energy emergent phenomenon, emerging after this coarse graining.
It is desirable though that we include gravity in trace dynamics, considering that Planck scale physics is involved. We also recall our other goal to have a formulation of quantum (field) theory without classical space-time. It turns out that the TD formalism can help us do that, if we can find a way to incorporate gravity. This would then also be a theory of quantum gravity. We also emphasised earlier that quantum gravity must dynamically explain the absence of space-time superpositions in the classical limit. That goal will be achieved here, because TD already has a mechanism (fluctuations) to explain spontaneous collapse.
So, how do we bring in gravity? It cannot be brought in simply as classical general relativity. That is not allowed by the Einstein hole argument: the matter in TD is not classical, whereas classical matter fields are needed to give operational meaning to the point structure of classical space-time. We also recall that trace dynamics describes matter degrees of freedom as matrices, which do not commute with each other. We search for a similar matrix/operator type description of gravity, which should not already be tied to quantisation of classical gravity. Because quantum theory should in fact emerge from the sought for [trace dynamics + gravity] after coarse-graining over Planck time scales. Thus we seek a matrix dynamics description of [matter + gravity], on the Planck scale.
Fortunately, such a matrix type description of gravity exists - it is the non-commutative geometry (NCG) program discovered and developed by Alain Connes and collaborators. From our point of view, keeping trace dynamics in mind, NCG could be introduced as follows: what kind of geometry would we get if we raised space-time points (described by real numbers) to the status of matrices/operators? Recall we did just this kind of thing for material particles and gauge fields in TD. Similarly, our space-time points now become operators, which in general do not commute with each other.
In a mathematical approach, this can be understood as follows. Physical space, or space-time, is described by the laws of geometry. It can be mapped to an algebra, by assigning coordinates to the points of space. Then geometric properties (such as curvature) can be described in terms of functions on the algebra. This of course is a commutative algebra - real numbers commute with each other. After mapping the geometry of the space to a (commutative) algebra, we now take the following step: we make the algebra non-commutative. This is precisely what is achieved by elevating points of the space (or space-time) to matrices. The matrices do not commute with each other, and hence we have a non-commutative algebra. Now we ask: what kind of geometry such a non-commutative algebra describe?! That `geometry’, we call non-commutative geometry. There is no corresponding geometry in the sense in which we relate geometry to space, but we can talk of analogous concepts: e.g. what is the curvature of a non-commutative space?
One immediately notices the striking parallel between trace dynamics on the one hand, and NCG on the other. Both obtain by elevating classical point structures to the status of non-commuting operators. The former arrives at a matrix dynamics for matter and gauge fields. The latter arrives at a matrix description of geometry. Now classical general relativity couples classical matter to Riemannian geometry: matter curves space-time. We then expect matter described by trace dynamics to couple to non-commutative geometry: matrix matter `curves’ non-commutative space-time. Thus we intend to built a matrix theory of matter + gravity by unifying trace dynamics with non-commutative geometry. And we demand that this matrix dynamics have the following properties: when we perform the statistical mechanics of this gravity-based matrix dynamics, we should obtain a quantum theory of gravity at equilibrium. Fluctuations should become important for macroscopic systems (macroscopic to be defined) and spontaneous collapse should then come into play, giving rise to an emergent classical space-time and classical matter fields, such that the classical space-time has a Riemannian geometry which obeys the laws of general relativity. Fortunately, a mathematical formalism for such a programme has been developed: this is the theory of Spontaneous Quantum Gravity (SQG). SQG is in fact trace dynamics + trace gravity (i.e. NCG). From here, quantum gravity, quantum (field) theory, and classical general relativity, and classical dynamics, are all emergent phenomena.
What would such a matrix gravity look like, mathematically? Naively, we might want to make coordinates into operators, raise each metric component to an operator, try to construct a curvature tensor operator, and somehow couple it to the trace Lagrangian for matter fields in TD. But this does not work, for various reasons. It is technically difficult to make an invariant four-volume from the determinant of the metric, when each metric component is an operator. It all does not have the right feel, to say the least. Furthermore, classical space-time has been lost; how will we even describe time evolution and hence the dynamics, in matrix gravity?
Fortunately, the formalism of NCG shows the way forward. One can properly describe concepts such as distance and metric, in a non-commutative geometry. What is very important is that NCG seems to provide a new fundamental time parameter - a property unique to non-commutative geometry, not found in commutative algebras. We will return to this in some detail in future posts - for now we just accept and employ this time parameter, which we will call Connes time. We lost space-time, but we recover time, and that is adequate for dynamics. Time is more fundamental than space.
When we raise space-time points to operators/matrices, like in TD, we can try to use the TD language of Grassmann matrices. In classical GR, metric is a field that lives on space-time. That won’t do now: trying to make something live on an operator. We expect the space-time operator to describe space-time geometry itself, and indeed that does happen. Also, we need to ask - the Grassmann matrix that represents space-time geometry: should it be just bosonic, or should it have a fermionic part too? I don’t at present know he answer to this important question. For now, we work with a Grassmann even (i.e. bosonic) matrix to describe spacetime geometry.
Since we want matrix gravity to yield GR (with matter sources) in the classical limit, we will have to specify a Lagrangian - both for gravity and for matter. Again, NCG shows the way, for gravity. There is a remarkable result in geometry, which relates curvature in a Riemannian geometry, to the Dirac operator on this space-time. Consider a Riemannian space - having a Euclidean signature. For now, and in this SQG program, we work with the Euclidean case. The Lorentzian case remains to be developed. Given a curved Riemannian space, one can write the standard Dirac operator DB on it [`gamma-mu del-mu’] in terms of the gamma-matrices and the spatial derivatives. A result from geometry states that [expressed for now as a simplified statement] the trace of the square of the Dirac operator is equal to the Einstein-Hilbert action [`integral of R root(g)’]. Isn’t that surprising - that the sum of the eigenvalues of the Dirac operator on a space is connected to Riemannian curvature on that space. The eigenvalues of the Dirac operator are connected to gravity - in fact they *are* gravity, as we will see later. The metric can be connected to these eigenvalues.
So we have this operator, DB2 on a Riemannian space. We can make the algebra of coordinates non-commutative, and we will still have this square of the Dirac operator: it describes curvature on a non-commutative space. And we nave the Connes time, labelled say tau, to describe evolution. We can now make contact with trace dynamics; recall that the trace Lagrangian is trace of an operator polynomial in configuration variables and their velocities. The trace polynomial coming from NCG is trace of square of the Dirac operator. Remembering that in quantum mechanics the Dirac operator is like momentum, we now introduce in our theory a bosonic operator/matrix qB such that its derivative with respect to Connes time is the Dirac operator DB. This is the defining condition for qB while the defining condition for the Dirac operator is as before: it becomes the ordinary Dirac operator on a Riemannian space, and there it relates to the Ricci scalar and the Einstein-Hilbert action. In matrix gravity, the action describing gravity is the (Connes) time integral of the trace of the squared Dirac operator. This has just the form expected from trace dynamics. Moreover, the Lagrange equation resulting from this action is also very simple: the momentum is constant in time, and the configuration variable evolves linearly with time.
Next, we must include matter, because we after all want to derive spontaneous localisation of matter, from the SQG theory. At this stage in this programme we consider matter fermions only, leaving the consideration of (bosonic) gauge fields and non-gravitational interactions for later. So we have to have a way to include say Dirac fermions, in the language of trace dynamics. One thing we can anticipate is that these will be described by fermionic Grassmann matrices. But what should the Lagrangian be, keeping also in mind that we also have the Dirac operator at hand. We could construct a trace Lagrangian for every fermion in the theory, add up these Lagrangians, and add this to the trace Lagrangian for gravity (described above), integrate it over Connes time, and that could give the action for matrix dynamics.
However, we do not go on that path, for conceptual reasons. Let us ask the question: what is the gravitational effect of an electron? An electron, being quantum mechanical, is all over space; so why must we distinguish the gravitational effect of the electron from the electron itself? This situation is unlike that of a classical object, say planet earth, where the object is localised in space, and its gravitational field is spread out everywhere. So we propose to introduce the concept of an `atom’ of space-time-matter [STM] which is a combined description of the fermionic part (say the electron) to be described by a fermionic operator qF, and its gravitation part, to be described by the bosonic qB. Thus, we define the operator q for an STM atom, written in terms of its bosonic and fermionic parts: q = qB + qF. For instance, in matrix gravity, an electron along with its gravity is an STM atom - it comes with its own operator space-time coordinates, its own Dirac operator. Further, we define the fermionic part of the Dirac operator, DF to be the Connes time derivative of qF. And the full Dirac operator D by D = DB + DF. Recall that the original Dirac operator DB is bosonic. The Lagrangian for an STM atom is the trace of the square of D, and the action is the time integral of this Lagrangian. There is one such term for each STM atom. We can write the total action for matrix gravity simply as:
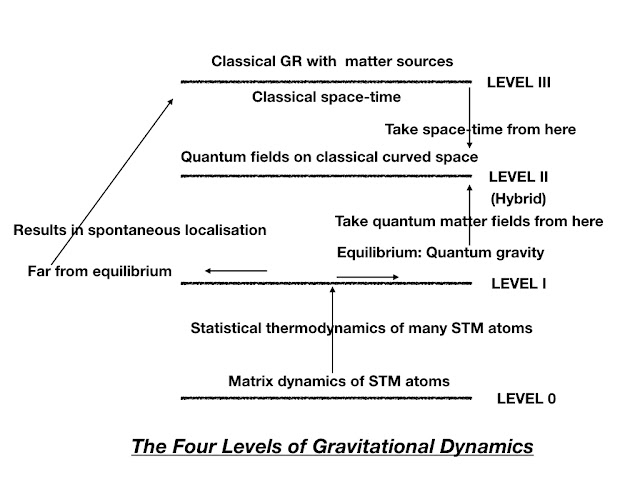
This is nice. From here we can derive quantum gravity, quantum theory, classical general relativity, all as emergent phenomena. To begin with, one easily obtains the Lagrange equations for the bosonic and fermionic part of each STM atom. The momenta are constant, and the configuration variables evolve linearly with time. Because of unitary invariance, there again is a conserved Adler-Millard charge. The following diagram helps us understand where to go next.
What we have described so far takes place at Level 0. There are only two fundamental constants at Level 0 - Planck length and Planck time. And there is the conserved Adler-Millard charge. Every STM atom has only one associated parameter, a length scale L, which eventually gets interpreted as Compton wavelength (L can be different for every atom). At Level 0, there is no Planck’s constant, no Newton’s gravitational constant, no concept of mass nor spin: all these are emergent at higher levels. At level 0, there is only the length scale L, from which mass and spin emerge subsequently at Level I. How do the STM atoms interact with each other? `Collisions’ and entanglement are possible mechanisms - this aspect is currently under investigation.
Level 0 is a Hilbert space on which the operators describing STM atoms live, and evolve in Connes time. Dynamics take place at the Planck scale, as in trace dynamics. There is no space-time here. Space-time and the laws of general relativity emerge at Level III, as a consequence of spontaneous localisation. We can say that space-time arises as a consequence of collapse of the wave-function; more specifically, the part of the wave function that describes the fermions. The bosonic part does not undergo localisation, and becomes space-time and its curvature.
Like in trace dynamics, we would like to know what the emergent dynamics at low energies is, if we average Level 0 dynamics over time scales much larger than Planck time. For this we perform the statistical thermodynamics of the STM atoms described by the action given in the equation above. What emerges, at equilibrium at Level I, are the standard quantum commutation relations, and Heisenberg equations of motion, separately for the bosonic and fermionic parts of each STM atom. Evolution is still in Connes time. Planck’s constant emerges too, and hence Newton’s gravitational constant can be defined, using Planck’s constant along with Planck time and Planck length. The mass of an STM atom is defined in terms of its length L, which length hence can be interpreted as its Compton wavelength. The Schwarzschild radius of an STM atom is defined as square of Planck length divided by L. One can transform to the Schrodinger picture dynamics as well, and define quantum entanglement. Thus what we have at equilibrium at Level I is a quantum theory of gravity, emergent from the Level 0 matrix gravity dynamics. If we would like to know what is the gravitation of an electron, we can answer that question at Level I, or at Level 0, but not at Level II or III. Note that this Level I quantum gravity is a low energy phenomenon! It does not have anything to do with the Planck scale, but rather comes into play whenever a background space-time is not available. This Level I quantum gravity is also the sought after description of quantum (field) theory without classical time.
If a sufficiently large number of STM atoms get entangled, something very interesting takes place. If the total mass of the entangled system of STM atoms goes above Planck mass, the effective Compton wavelength of the full system goes below Planck length. The approximation that we can coarse grain the Level 0 dynamics over times larger than Planck times breaks down. This is what we mean by fluctuations becoming important. The entangled system experiences rapid Planck scale fluctuations, an anti-self-adjoint part from the fermionic trace Hamiltonian is no longer negligible, and the entangled system undergoes extremely rapid spontaneous localisation. The localisation of the fermionic parts of many such entangled systems gives rise to the macroscopic bodies of the universe. Their bosonic parts together describe classical gravity, which is shown to obey the laws of classical general relativity.
Those STM atoms which do not undergo spontaneous localisation are to be described at Level 0 or Level I. Or, if we neglect their gravity, we can describe them at the hybrid Level II, after borrowing the space-time part from Level III. This is how we conventionally do quantum (field) theory.
The theory of Spontaneous Quantum Gravity makes the following predictions:
1. Spontaneous localisation (the GRW theory) is a prediction of this theory, and the GRW theory is being tested in labs currently. If the GRW theory is ruled out by experiments, this proposal will be ruled out too.
2. SQG predicts the novel phenomena of quantum interference in time, and spontaneous collapse in time.
3.The theory predicts the Karolyhazy length as a minimum length. This is testable and falsifiable.
4. This theory predicts that dark energy is a quantum gravitational phenomenon.
5. The theory provides an explanation for black hole entropy, from the microstates of STM atoms.
In forthcoming posts, we will discuss the SQG theory as well as its predictions in some detail. SQG is a candidate cover theory for general relativity, in the sense discussed in the first post. It explains the emergence of the classical world from quantum gravity, without having to resort to any interpretation of quantum mechanics.

No comments:
Post a Comment
The purpose of this blog is to have a discussion on the connection between quantum foundations and quantum gravity. Students and professionals working on or interested in these subjects are very welcome to participate. Please post only on this or related topics. Off-topic comments will be removed. Obscene, vulgar and abusive posts will be removed.